Write a C Program to Construct the Minimum Spanning Tree Using the Prim’s Algorithm

by

Aim:

To construct the minimum spanning tree using Prim’s Algorithm.

Theory:

  • Given a connected and undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together.
  • A single graph can have many different spanning trees. A minimum spanning tree (MST) or minimum weight spanning tree for a weighted, connected and undirected graph is a spanning tree with weight less than or equal to the weight of every other spanning tree.
  • The weight of a spanning tree is the sum of weights given to each edge of the spanning tree.

Prim’s Algorithm

  • Prim’s Algorithm also uses the Greedy approach to find the minimum spanning tree.
  • In Prim’s Algorithm, we grow the spanning tree from a starting position.
  • Unlike an edge in Kruskal’s, we add a vertex to the growing spanning tree in Prim’s.

Algorithm:

  • Maintain two disjoint sets of vertices. One containing vertices that are in the growing spanning tree and other that are not in the growing spanning tree.
  • Select the cheapest vertex that is connected to the growing spanning tree and is not in the growing spanning tree and add it into the growing spanning tree. This can be done using Priority Queues. Insert the vertices that are connected to growing spanning tree, into the Priority Queue.
  • Check for cycles. To do that, mark the nodes which have been already selected and insert only those nodes in the Priority Queue that are not marked.

Consider the example below:

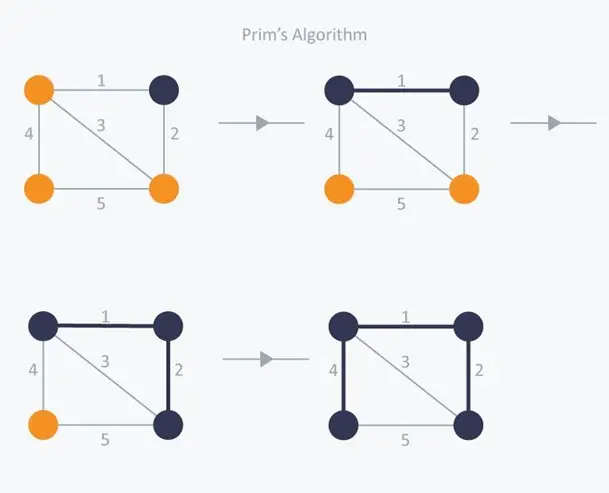
  • In Prim’s Algorithm, we will start with an arbitrary node (it doesn’t matter which one) and mark it. In each iteration we will mark a new vertex that is adjacent to the one that we have already marked.
  • As a greedy algorithm, Prim’s algorithm will select the cheapest edge and mark the vertex.
  • So we will simply choose the edge with weight 1.
  • In the next iteration we have three options, edges with weight 2, 3 and 4.
  • So, we will select the edge with weight 2 and mark the vertex.
  • Now again we have three options, edges with weight 3, 4 and 5.
  • But we can’t choose edge with weight 3 as it is creating a cycle.
  • So we will select the edge with weight 4 and we end up with the minimum spanning tree of total cost 7 (= 1 + 2 +4).

Program:

#include<stdio.h>
#include<stdlib.h>
#define infinity 999
#define MAX 20
int G[MAX][MAX],spanning[MAX][MAX],n;
int prims();
int main()
{
int i,j,total_cost;
printf("Enter no. of vertices:");
scanf("%d",&n);
printf("\nEnter the adjacency matrix:\n");
for(i=0;i<n;i++)
for(j=0;j<n;j++)
scanf("%d",&G[i][j]);
total_cost=prims();
printf("\nspanning tree matrix:\n");
for(i=0;i<n;i++)
{
printf("\n");

for(j=0;j<n;j++)
printf("%d\t",spanning[i][j]);
}
printf("\n\nTotal cost of spanning tree=%d",total_cost);
return 0;
}
int prims()
{
int cost[MAX][MAX];
int u,v,min_distance,distance[MAX],from[MAX];
int visited[MAX],no_of_edges,i,min_cost,j;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
{
if(G[i][j]==0)
cost[i][j]=infinity;
else
cost[i][j]=G[i][j];
spanning[i][j]=0;
}

distance[0]=0;
visited[0]=1;
for(i=1;i<n;i++)
{
distance[i]=cost[0][i];
from[i]=0;
visited[i]=0;
}
min_cost=0; //cost of spanning tree
no_of_edges=n-1; //no. of edges to be added
while(no_of_edges>0)
{

min_distance=infinity;
for(i=1;i<n;i++)
if(visited[i]==0&&distance[i]<min_distance)
{
v=i;
min_distance=distance[i];
}
u=from[v];

spanning[u][v]=distance[v];
spanning[v][u]=distance[v];
no_of_edges--;
visited[v]=1;
//updated the distance[] array
for(i=1;i<n;i++)
if(visited[i]==0&&cost[i][v]<distance[i])
{
distance[i]=cost[i][v];
from[i]=v;
}
min_cost=min_cost+cost[u][v];
}
return(min_cost);
}

Execution:

Input:
5 1 5 2 8 6 0 4 7 5 1 9 6 4 7 0 6 3 0 6 1 7 5 3 6 0

Output:

Enter no. of vertices:
Enter the adjacency matrix:

spanning tree matrix:

0	0	2	0	0	
0	0	0	0	1	
2	0	0	0	3	
0	0	0	0	1	
0	1	3	1	0	

Total cost of spanning tree=1012

Result:

Thus, construct the minimum spanning tree using Prim’s Algorithm was executed successfully.

Leave a Comment