Aim:
To Write a C Program to Implement Binary Search Trees Using Linked Lists.
Theory:
Binary Search Trees:
A binary tree is a tree in which no node can have more than two children. In a binary search tree ,for every node, X, in the tree, the values of all the keys in its left sub tree are smaller than the key value of X, and the values of all the keys in its right sub tree are larger than the key value of X. The basic operations on a binary search tree take time proportional to the height of the tree.
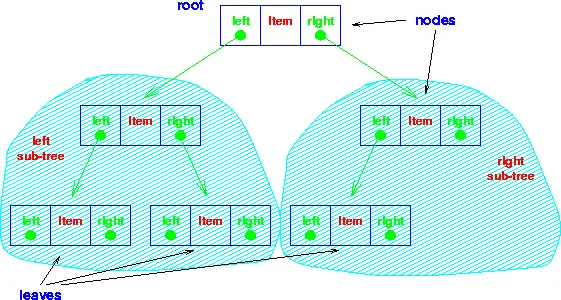
In the linked list implementation of binary search trees: Each element is represented by node with two link fields and a data field. Each connecting line (or edge) in a binary tree drawing will be represented by a link field. A leaf node has a leftChild and rightChild link of NULL. Root node will be pointed to by a pointer variable.
Algorithm:
- Create a structure with an element (Element) and two pointers – Left and Right that points to the left and right child node respectively in the tree.
- Create a new node using malloc function and assign the resultant pointer variable to the root node pointer T and assign it to NULL.
- To insert a new element X into the tree:
- If the value of T is NULL, assign T->Element to X, and the left and right child pointers to NULL and exit the insertion operation.
- Otherwise if the element to be inserted is less than the root element T, repeat the step 3 recursively, with the new value of T as T->Left.
- Otherwise if the element to be inserted is more than the root element T, repeat the step 3 recursively, with the new value of T as T->Right.
- If the element is already present in the tree, do nothing.
- To delete an element X from the tree:
- Find the node where the element resides.
- If the node has no left and right children, then the pointer to that node from the parent is changed to NULL and the node is freed of its memory.
- If the node has only one child, then the parent of the node is made to point to the child of the node and the node is freed.
- If the node has both left and right children:
- Look at the right subtree of the node (subtree rooted at the right child of the node).
- Find the Minimum there.
- Replace the key of the node to be deleted by the minimum element.
- Delete the minimum element.
- To find an element X in the tree with root node T:
- If the root node T is initially NULL, then the tree is empty. So return NULL and exit.
- Take element X and compare it with the root node. If X is less than the element found at the root node, then repeat step 5 recursively with the new value of T as T->Left. Take element X and compare it with the root node. If X is more than the element found at the root node, then repeat step 5 recursively with the new value of T as T->Right.
- To find the minimum element in a tree with root node T:
- If T is NULL return NULL.
- Otherwise slide the value of T to T->Left until T->Left becomes NULL.
- Return the value of T.
- To find the maximum element in a tree with root node T:
- If T is NULL return NULL.
- Otherwise, slide the value of T to T->Right until T->Right becomes NULL.
- Return the value of T.
Program:
#include<stdio.h>
#include<stdlib.h>
struct Treenode;
typedef struct Treenode *Position;
typedef struct Treenode *SearchTree;
SearchTree Insert(int X,SearchTree T);
SearchTree Delete(int X,SearchTree T);
Position Find(int X,SearchTree T);
Position FindMin(SearchTree T);
Position FindMax(SearchTree T);
void Display(SearchTree T);
struct Treenode
{
int Element;
SearchTree Left;
SearchTree Right;
};
Position T,P;
void main()
{
int X,op=1;
T=NULL;
do
{
printf("\n\n\t\t\t BST :MAIN MENU");
printf("\n\n\n\t1.INSERTION\n\t2.DELETE\n\t3.SEARCH\n\t4.SEARCH MINIMUM VALUE\n\t5.FIND MAXIMUM VALUE\n\t6.DISPLAY\n\t7.EXIT\n");
printf("\n\n\tENTER YOUR CHOICE :");
scanf("%d",&op);
switch(op)
{
case 1:printf("\n\n\tEnter the element\n");
scanf("%d",&X);
T=Insert(X,T);
printf("\n\n\tNew element is inserted\n ");
break;
case 2:printf("\n\n\tEnter the element to delete");
scanf("%d",&X);
P=Delete(X,T);
printf("\n\n\tElement at position %d is deleted\n",P);
break;
case 3:printf("\n\n\tEnter the element to find");
scanf("%d",&X);
P=Find(X,T);
if(P==NULL)
printf("\n\n\tThe element is not found\n");
else
printf("\n\n\tThe element is found at position %d\n",P);
break;
case 4:P=FindMin(T);
printf("\n\n\tThe minimum element in the tree is %d and it is found at position %d\n",P->Element,P);
break;
case 5:P=FindMax(T);
printf("\n\n\tThe maximum element in the tree is %d and it is found at position %d\n",P->Element,P);
break;
case 6:Display(T);
break;
case 7:exit(0);
break;
}
}while(op!=7);
}
SearchTree Insert(int X,SearchTree T)
{
if(T==NULL)
{
T=(SearchTree)malloc(sizeof(struct Treenode));
T->Element=X;
T->Left=T->Right=NULL;
}
else if(X<T->Element)
T->Left=Insert(X,T->Left);
else if(X>T->Element)
T->Right=Insert(X,T->Right);
return T;
}
Position Find(int X,SearchTree T)
{
if(T==NULL)
return NULL;
if(X<T->Element)
return Find(X,T->Left);
else if(X>T->Element)
return Find(X,T->Right);
else
return T;
}
Position FindMin(SearchTree T)
{
if(T==NULL)
return NULL;
else if(T->Left==NULL)
return T;
else
return FindMin(T->Left);
}
Position FindMax(SearchTree T)
{
if(T==NULL)
return NULL;
else if(T->Right==NULL)
return T;
else
return FindMax(T->Right);
}
SearchTree Delete(int X, SearchTree T)
{
Position TmpCell;
if(T==NULL)
printf("Element not found\n");
else if(X<T->Element)
T->Left=Delete(X,T->Left);
else if(X>T->Element)
T->Right=Delete(X,T->Right);
else if(T->Left && T->Right)
{
TmpCell=FindMin(T->Right);
T->Element=TmpCell->Element;
T->Right=Delete(T->Element,T->Right);
}
else
{
TmpCell=T;
if(T->Left==NULL)
T=T->Right;
else if(T->Right==NULL)
T=T->Left;
free(TmpCell);
}
return T;
}
void Display(SearchTree T)
{
//printf("\nADD\tVALUE\n");
if(T!=NULL)
{
Display(T->Left);
printf("%d\t%d\n",T,T->Element);
Display(T->Right);
}
}
Execution:
Input: 1 45 1 67 1 654 1 34 2 45 3 67 4 5 6 Output: BST :MAIN MENU 1.INSERTION 2.DELETE 3.SEARCH 4.SEARCH MINIMUM VALUE 5.FIND MAXIMUM VALUE 6.DISPLAY 7.EXIT ENTER YOUR CHOICE : Enter the element New element is inserted BST :MAIN MENU 1.INSERTION 2.DELETE 3.SEARCH 4.SEARCH MINIMUM VALUE 5.FIND MAXIMUM VALUE 6.DISPLAY 7.EXIT ENTER YOUR CHOICE : Enter the element New element is inserted BST :MAIN MENU 1.INSERTION 2.DELETE 3.SEARCH 4.SEARCH MINIMUM VALUE 5.FIND MAXIMUM VALUE 6.DISPLAY 7.EXIT ENTER YOUR CHOICE : Enter the element New element is inserted BST :MAIN MENU 1.INSERTION 2.DELETE 3.SEARCH 4.SEARCH MINIMUM VALUE 5.FIND MAXIMUM VALUE 6.DISPLAY 7.EXIT ENTER YOUR CHOICE : Enter the element New element is inserted BST :MAIN MENU 1.INSERTION 2.DELETE 3.SEARCH 4.SEARCH MINIMUM VALUE 5.FIND MAXIMUM VALUE 6.DISPLAY 7.EXIT ENTER YOUR CHOICE : Enter the element to delete Element at position 27131920 is deleted BST :MAIN MENU 1.INSERTION 2.DELETE 3.SEARCH 4.SEARCH MINIMUM VALUE 5.FIND MAXIMUM VALUE 6.DISPLAY 7.EXIT ENTER YOUR CHOICE : Enter the element to find The element is found at position 27131920 BST :MAIN MENU 1.INSERTION 2.DELETE 3.SEARCH 4.SEARCH MINIMUM VALUE 5.FIND MAXIMUM VALUE 6.DISPLAY 7.EXIT ENTER YOUR CHOICE : The minimum element in the tree is 34 and it is found at position 27132016 BST :MAIN MENU 1.INSERTION 2.DELETE 3.SEARCH 4.SEARCH MINIMUM VALUE 5.FIND MAXIMUM VALUE 6.DISPLAY 7.EXIT ENTER YOUR CHOICE : The maximum element in the tree is 654 and it is found at position 27131984 BST :MAIN MENU 1.INSERTION 2.DELETE 3.SEARCH 4.SEARCH MINIMUM VALUE 5.FIND MAXIMUM VALUE 6.DISPLAY 7.EXIT ENTER YOUR CHOICE :27132016 34 27131920 67 27131984 654 BST :MAIN MENU 1.INSERTION 2.DELETE 3.SEARCH 4.SEARCH MINIMUM VALUE 5.FIND MAXIMUM VALUE 6.DISPLAY 7.EXIT ENTER YOUR CHOICE :
Result:
Thus, Implementation of Binary search tree was executed Successfully.

