To Write a C Program to Implement an Expression Tree Using Tree Traversals Technique

by

Aim:

To write a C Program to Implement an Expression Tree Using Tree Traversals Technique. Produce its pre-order, in-order, and post-order traversals.

Theory:

Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree. There are three ways which we use to traverse a tree:

  • In-order Traversal
  • Pre-order Traversal
  • Post-order Traversal

Generally, we traverse a tree to search or locate a given item or key in the tree or to print all the values it contains.

In-order Traversal:

  • In this traversal method, the left subtree is visited first, then the root and later the right sub-tree.
  • We should always remember that every node may represent a subtree itself.
  • If a binary tree is traversed in order, the output will produce sorted key values in ascending order.

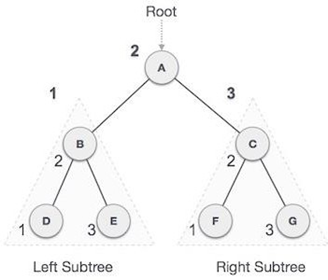
We start from A, and following in-order traversal, we move to its left subtree B. B is also traversed in-order. The process goes on until all the nodes are visited. The output of inorder traversal of this tree will be:

D → B → E → A → F → C → G

Algorithm:

Until all nodes are traversed :

  • Step 1 − Recursively traverse left subtree.
  • Step 2 − Visit root node.
  • Step 3 − Recursively traverse right subtree.

Pre-order Traversal:

In this traversal method, the root node is visited first, then the left subtree and finally the right subtree.

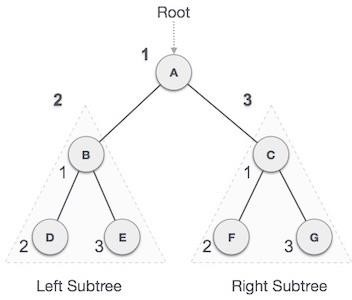
We start from A, and following pre-order traversal, we first visit A itself and then move to its left subtree B. B is also traversed pre-order. The process goes on until all the nodes are visited. The output of pre-order traversal of this tree will be :

A → B → D → E → C → F → G

Algorithm:

Until all nodes are traversed :

  • Step 1 − Visit the root node.
  • Step 2 − Recursively traverse the left subtree.
  • Step 3 − Recursively traverse the right subtree.

Post-order Traversal:

In this traversal method, the root node is visited last, hence the name. First we traverse the left subtree, then the right subtree and finally the root node.

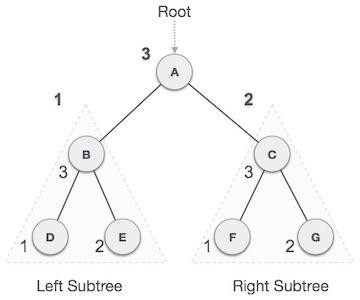
We start from A, and following Post-order traversal, we first visit the left subtree B. B is also traversed post-order. The process goes on until all the nodes are visited. The output of post-order traversal of this tree will be :

D → E → B → F → G → C → A

Algorithm:

Until all nodes are traversed :

  • Step 1 − Recursively traverse left subtree.
  • Step 2 − Recursively traverse right subtree.
  • Step 3 − Visit root node.

Program:

#include <stdio.h>
#include <stdlib.h>
struct node {
int data; 	
struct node *leftChild;
struct node *rightChild;
};
struct node *root = NULL;
void insert(int data) {
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL; 
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) { 
parent = current;                
if(data < parent->data) {
current = current->leftChild;                            
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
} 
else {
current = current->rightChild;         
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}            
}
}
struct node* search(int data) {
struct node *current = root;
printf("Visiting elements: ");
while(current->data != data) {
if(current != NULL)
printf("%d ",current->data); 
if(current->data > data) {
current = current->leftChild;
}
else {                
current = current->rightChild;
}
if(current == NULL) {
return NULL;
}
}
return current;
}
void pre_order_traversal(struct node* root) {
if(root != NULL) {
printf("%d ",root->data);
pre_order_traversal(root->leftChild);
pre_order_traversal(root->rightChild);
}
}

void inorder_traversal(struct node* root) {
if(root != NULL) {
inorder_traversal(root->leftChild);
printf("%d ",root->data);          
inorder_traversal(root->rightChild);
}
}

void post_order_traversal(struct node* root) {
if(root != NULL) {
post_order_traversal(root->leftChild);
post_order_traversal(root->rightChild);
printf("%d ", root->data);
}
}
int main() {
int i;
int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
for(i = 0; i < 7; i++)
insert(array[i]);
i = 31;
struct node * temp = search(i);
if(temp != NULL) {
printf("[%d] Element found.", temp->data);
printf("\n");
}else {
printf("[ x ] Element not found (%d).\n", i);
}
i = 15;
temp = search(i);
if(temp != NULL) {
printf("[%d] Element found.", temp->data);
printf("\n");
}else {
printf("[ x ] Element not found (%d).\n", i);
}            
printf("\nPreorder traversal: ");
pre_order_traversal(root);
printf("\nInorder traversal: ");
inorder_traversal(root);
printf("\nPost order traversal: ");
post_order_traversal(root);       
return 0;
}

Execution:

Input:
27 14 10 19 35 31 42

Output:
Visiting elements: 27 35 [31] Element found.
Visiting elements: 27 14 19 [ x ] Element not found (15).

Preorder traversal: 27 14 10 19 35 31 42 
Inorder traversal: 10 14 19 27 31 35 42 
Post order traversal: 10 19 14 31 42 35 27

Result:

Thus, Implement of Tree traversal was executed successfully.

Leave a Comment