Given two (singly) linked lists, determine if the two lists intersect and return the intersecting node

by

QUESTION:

Intersection: Given two (singly) linked lists, determine if the two lists intersect. Return the intersecting node. Note that the intersection is defined based on reference, not value. That is, if the kth node of the first linked list is the exact same node (by reference) as the jth node of the second linked list, then they are intersecting.

SOLUTION:

  • Let’s draw a picture of intersecting linked lists to get a better feel for what is going on.
  • Here is a picture of intersecting linked lists:

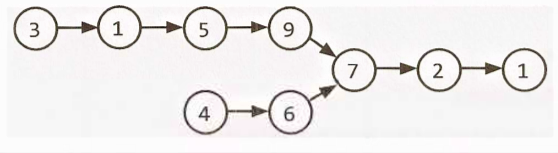
And here is a picture of non-intersecting linked lists:

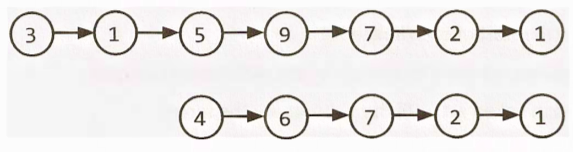
  • We should be careful here to not inadvertently draw a special case by making the linked lists the same length.
  • Let’s first ask how we would determine if two linked lists intersect.

Determining if there’s an intersection.

  • How would we detect if two linked lists intersect? One approach would be to use a hash table and just throw all the linked lists nodes into there. We would need to be careful to reference the linked lists by their memory location, not by their value.
  • There’s an easier way though. Observe that two intersecting linked lists will always have the same last node.
  • Therefore, we can just traverse to the end of each linked list and compare the last nodes.
  • How do we find where the intersection is, though?

Finding the intersecting node.

  • One thought is that we could traverse backwards through each linked list. When the linked lists”split’; that’s the intersection.
  • Of course, you can’t really traverse backwards through a singly linked list.
  • If the linked lists were the same length, you could just traverse through them at the same time.
  • When they collide, that’s your intersection.
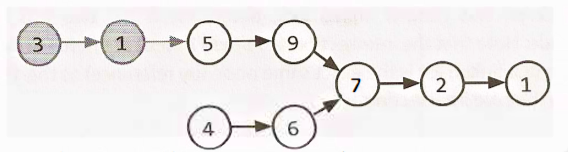
  • When they’re not the same length, we’d like to just”chop off”-or ignore-those excess (gray) nodes.
  • How can we do this? Well, if we know the lengths of the two linked lists, then the difference between those two linked lists will tell us how much to chop off.
  • We can get the lengths at the same time as we get the tails of the linked lists (which we used in the first step to determine if there’s an intersection).

Putting it all together:

We now have a multistep process.

  1. Run through each linked list to get the lengths and the tails.
  2. Compare the tails. If they are different (by reference, not by value), return immediately. There is no inter
    section.
  3. Set two pointers to the start of each linked list.
  4. On the longer linked list, advance its pointer by the difference in lengths.
  5. Now, traverse on each linked list until the pointers are the same.

The implementation for this is below.

LinkedlistNode findintersection(LinkedListNode listl, LinkedListNode list2) {
if (listl == null I I list2 == null) return null;

/* Get tail and sizes. */
Result resultl getTailAndSize(listl);
Result result2 = getTailAndSize(list2);

/* If different tail nodes, then there's no intersection. */
if (resultl.tail != result2.tail) {
return null;
}

/* Set pointers to the start of each linked list. */
LinkedlistNode shorter = resultl.size < result2.size? listl : list2;
LinkedlistNode longer = resultl.size < result2.size ? list2 : listl;

/* Advance the pointer for the longer linked list by difference in lengths. */
longer = getKthNode(longer, Math.abs(resultl.size - result2.size));

/* Move both pointers until you have a collision. */
while (shorter != longer) {
}
shorter = shorter.next;
longer = longer.next;

/* Return either one. */
return longer;
}
class Result {
public LinkedlistNode tail;
public int size;
public Result(LinkedListNode tail, int size) {
this.tail tail;
this.size= size;
}
}
Result getTailAndSize(LinkedListNode list) {
if (list == null) return null;
int size = 1;
LinkedlistNode current= list;
while (current.next != null) {
size++;
current = current.next;
}
return new Result(current, size);
}
LinkedListNode getKthNode(LinkedListNode head, int k) {
LinkedListNode current= head;
while (k > 0 && current != null) {
current = current.next;
k--;
}
return current;
}

This algorithm takes O(A + B) time, where A and Bare the lengths of the two linked lists. It takes O(1) additional space.

Leave a Comment