Given an image represented by an NxN matrix, where each pixel in the image is 4 bytes, write a method to rotate the image by 90 degrees

QUESTION:

Rotate Matrix: Given an image represented by an NxN matrix, where each pixel in the image is 4 bytes, write a method to rotate the image by 90 degrees. Can you do this in place?

SOLUTION:

• Because we’re rotating the matrix by 90 degrees, the easiest way to do this is to implement the rotation in layers.
• We perform a circular rotation on each layer, moving the top edge to the right edge, the right edge to the bottom edge, the bottom edge to the left edge, and the left edge to the top edge.

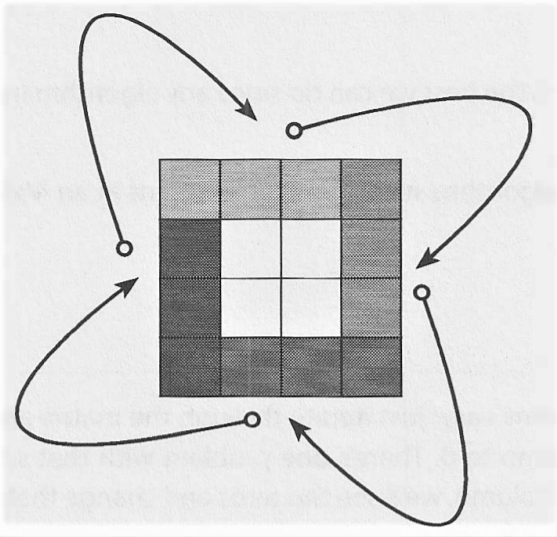
• How do we perform this four-way edge swap? One option is to copy the top edge to an array, and then move the left to the top, the bottom to the left, and so on.
• This requires O(N) memory, which is actually unnecessary.

A better way to do this is to implement the swap index by index. In this case, we do the following:

for i = 0 to n
temp= top[i];
top[i] = left[i]
left[i] = bottom[i]
bottom[i] = right[i]
right[i] = temp 

We perform such a swap on each layer, starting from the outermost layer and working our way inwards. (Alternatively, we could start from the inner layer and work outwards.)

The code for this algorithm is below.

boolean rotate(int[][] matrix) {
if (matrix.length== 0 I I matrix.length != matrix[0].length) return false;
int n = matrix.length;
for (int layer = 0; layer < n / 2; layer++) {
int first= layer;
int last= n - 1 - layer;
for(int i = first; i < last; i++) {
int offset = i - first;
int top= matrix[first][i]; //save top
//left -> top
matrix[first][i] matrix[last-offset][first];
//bottom -> left
matrix[last-offset][first]
//right -> bottom
matrix[last][last offset]
//top -> right
matrix[last][last - offset];
matrix[i][last];
matrix[i][last] top; // right<- saved top
}
}
return true;
}

This algorithm is O (N²), which is the best we can do since any algorithm must touch all N² elements.